The Kaplansky unit conjecture, perhaps the most popular of three algebra inquiries named after American mathematician Irving Kaplansky, has been disproved by a researcher showing a counterexample after more than 80 years.
Postdoctoral researcher and mathematician Giles Gardam first announced the disproof as an unexpected twist in his hour-long virtual talk on Kaplansky's conjectures last February 22. He then noted how these notions related to the K-theory, a part of mathematics that focuses on rings generated by vector bundles over a topological space.
Gardam also presents his proof against the unit conjecture in a paper titled "A counterexample to the unit conjecture for group rings" available on the preprint repository arXiv.
The Longevity of Kaplansky's Conjectures
Explaining the Kaplansky unit conjecture in simpler terms, the problem is likened to finding multiplicative inverses in a "broad family of algebraic structures."
Multiplicative inverses are pairs of numbers that give one as its products, which is the case for any number and its reciprocal like 2 and ½. However, the unit conjecture does not concern itself simply with integers, but with elements from "group algebra." This covers the presence of fields and groups and the linear combinations of the two elements, combining a number system (like real numbers or clock arithmetic systems) with a group (a collection of finite or infinite elements such as matrices and symmetry transformations).
In these group algebra structures, mathematicians from 80 years ago believed that only the simplest elements could have reciprocals or multiplicative inverses.
Over the years, the unit conjecture, together with two other Kaplansky's conjectures (the zero divisor conjecture and the idempotent conjecture), came to be treated as "hopeless things," according to Dawid Kielak from the University of Oxford. However, these algebra problems remained a part of future mathematical studies mainly because of their relevance to K-theory.
Unit Conjecture is False
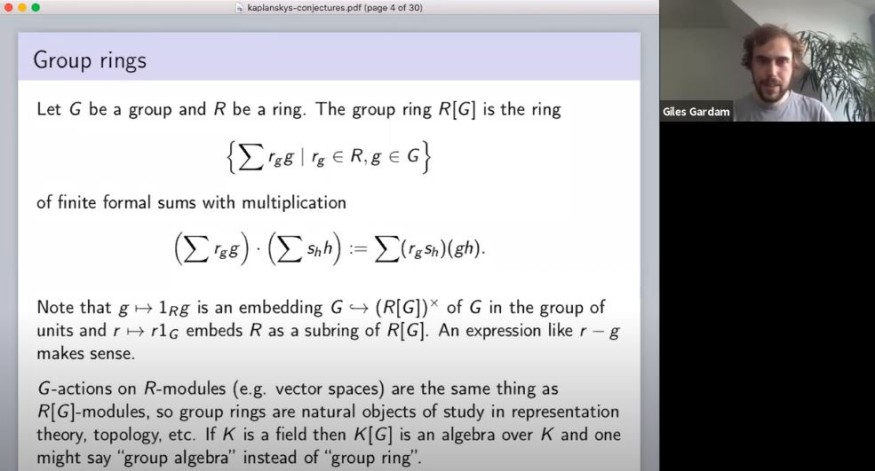
As a part of the Symmetry in Newcastle online series from the University of Newcastle in Australia, Gardam explained the history of Kaplansky's conjectures before going further on the unit conjecture. Kaplansky's unit conjecture predicts that if K is a field and G is a torsion-free group, then the group ring K[G] must have no zero divisors, with the only units being trivial units - the non-zero scalar multiples of its elements.
Near the end of his online lecture, Giles Gardam revealed: "I'm really happy to be able to announce today, for the first time, that in fact, the unit conjecture is false."
While he did not reveal how he uncovered the counterexample that solved an 80-year-old problem, he told online publication Quanta that he would share additional details in the following months.
"I'm still optimistic that maybe I have enough tricks left to get some more results," Gardam tells Quanta.
Giles Gardam, from the University of Münster in Germany, disproved the unit conjecture by presenting unusual "units," which are elements that have multiplicative inverses within a group algebra generated from the symmetries of a specific 3D crystallographic shape. A model showing this crystallographic group, and its 21 group elements are presented through visualization on Quanta mag. Additionally, Gardam demonstrates that the counterexample is "virtually abelian" with a field being of order two.
RELATED ARTICLE: 3 Statistical Facts That Seem Outrageous at First
Check out more news and information on Mathematics in Science Times.